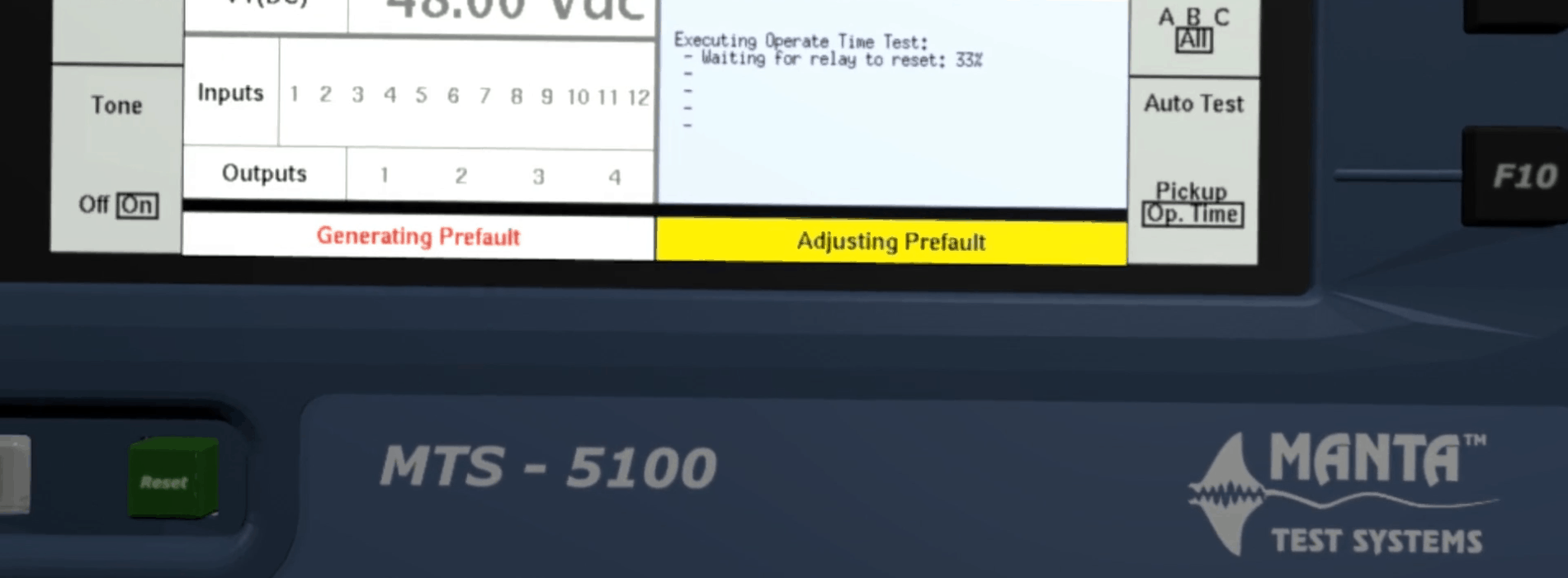
Symmetrical Components Made Easy – Part 1
Before computer software applications, the task of calculating fault currents for a three-phase electrical system was a challenging task. A mathematical theorem using symmetrical components and sequence networks was the most practical method to conduct fault studies. Although we now have computers systems to calculate and perform in-depth fault and coordination studies, there is still a need to for a thorough understanding of these theoretical components. Modern protective relays calculate symmetrical components and use these values for protection settings and logic.
There are three symmetrical components: positive, negative and zero sequence. The general equations to determine these sequence quantities from a three-phase system, are as follows:

Positive sequence components in a non-faulted, three-phase power system
Below is a phasor diagram of a balanced, non-faulted three-phase power system. The phases are equal in amplitude and phase angle. The following set of drawings pictorially calculates the amount of positive sequence component in a balance system. The vector addition of 120°and 240° corresponds to the “a” and “a2” constants in the positive sequence formula above.
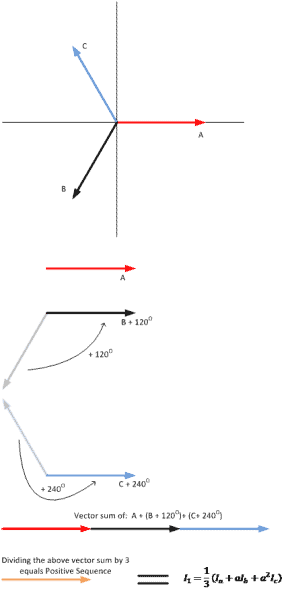
Thus, the positive sequence component in a non-faulted, balanced system is equal to one of the phases.
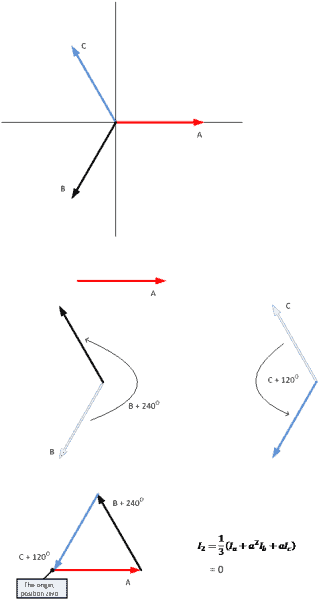
Negative sequence components in a non-faulted, three-phase power system
Performing the same phasor calculation, we can determine the amount of negative sequence component in a non-faulted, balanced three-phase power system. The negative sequence formula is proven.
Adding “a” and “a2” to the appropriate phasors, as per the negative sequence formula, then adding the phasor by placing the arrow tip to arrow tail results in a return to zero position. Thus, there is no negative sequence component in a non-faulted, three-phase system.

Zero sequence components in a non-faulted, three-phase power system
Lastly, we calculate the amount of zero sequence component in the same three-phase system. The formula for zero sequence is straight forward, in that there is no angle addition (i.e. no “a” or “a2“) and is simply phasor addition by placing the phasors “tip to tail.”
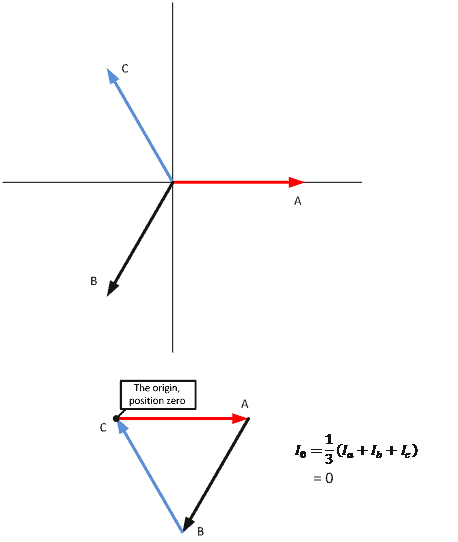
Thus, there is no zero-sequence component in a non-faulted, balanced three-phase system.
Conclusion:
- Strong knowledge and understanding of symmetrical components is key to testing and troubleshooting power system protection.
- Symmetrical components are calculated and formulas are proven by phasor diagrams.
- There is only positive sequence in a balanced three-phase system – no negative sequence or zero sequence.
In the next post we will examine the sequence components of a phase to ground fault.